Maximum of free damped oscillators

While reading a blog entry on free damped oscillators by Dr. Drang, I was caught off guard by the fact that the maximum of the damped oscillation solution is different from the envelope that is tangent to it. Looking back, this was obviously since the exponential is a monotonic decreasing function which would change the position of the local maximum of the cosine function. What I took for granted was the fact that the distance between the maximum is the same as the period of the cosine function.

The solution of the free damped oscillator is

$$ x(t) = Ae^{-\eta t}\cos(\omega t - \phi), $$

where $\eta$ is a damping constant, $A$ is the amplitude, $\omega$ is the angular frequency, and $\phi$ is a phase shift that depends on initial conditions. With $\eta=0.5$, $\omega=2\pi$, and $\phi=0$, this function looks like this:

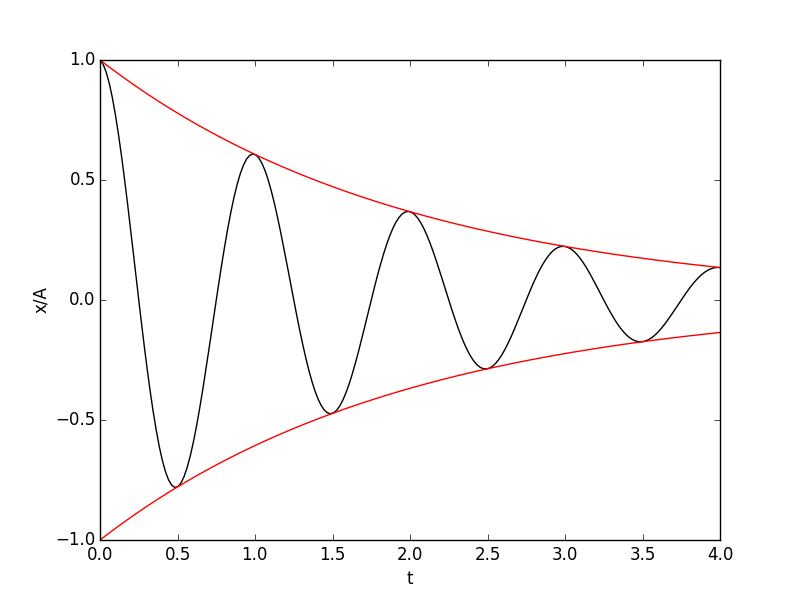
Free damped oscillator

The red function is $\pm e^{-\eta t}$, which is the envelope for $x(t)$ (the middle function). If you zoom into the peak at $t=1$, the difference between the peak of $x(t)$ and the envelope is apparent:

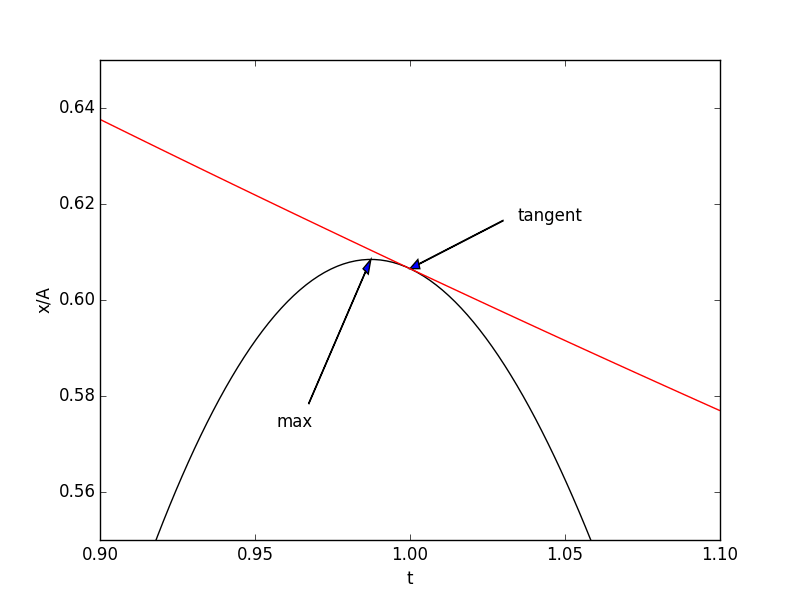
Free damped oscillator zoom

What is the actual difference between them? Well that just takes some simple calculus:

$$ \dfrac{dx}{dt} = -\eta\omega A e^{-\eta t}\cos(\omega t-\phi) - \omega A e^{-\eta t}\sin(\omega t -\phi) $$

Then taking the derivative and setting it equal to zero:

$$ -\eta\omega A e^{-\eta t}\cos(\omega t-\phi) - \omega A e^{-\eta t}\sin(\omega t -\phi) = 0 $$

and solving for $t$:

$$ t_{max} = -\dfrac{1}{\omega}\arctan(\eta) + \dfrac{\phi+2\pi n}{\omega} $$

where $n$ is a natural number. The tagent value can be obtained by setting $x(t)$ equal to the envelope:

$$ Ae^{-\eta t} = Ae^{-\eta t}\cos(\omega t - \phi) $$

and then solving for $t$:

$$ t_{tang} = \dfrac{\phi + 2 \pi n}{\omega} $$

where $n$ is a natural number. These are the maximum values for a normal cosine function.

Summary

The difference between $t_{max}$ and $t_{tang}$ is:

$$ t_{tang}-t_{max} = \dfrac{1}{\omega}\arctan(\eta) $$

This difference is the same for every peak, thus distance between the maximum of $x(t)$ is the same as the period of the cosine function. Honestly, this post is not that revolutionary, but I just wanted to test out how math renders on my site.

Code for Plots

For those who are interested, I used matplotlib to generated the graphs above:

import matplotlib.pyplot as plt
from numpy import exp, cos, pi, linspace
from scipy.optimize import minimize

eta = 0.5
omega = 2 * pi


def damped_os(t):
    return exp(-eta * t) * cos(omega * t)

t = linspace(0, 4, num=2000)
x = damped_os(t)
x_u = exp(-eta * t)
x_d = -exp(-eta * t)

fig, axes = plt.subplots()
axes.plot(t, x, 'black')
axes.plot(t, x_u, 'red')
axes.plot(t, x_d, 'red')

axes.set_xlabel('t')
axes.set_ylabel('x/A')

# plt.savefig('{filename}/images/201405_Maximum_of_damped_free_vibrations/freedampedfull.png')

# Zooming
axes.set_xlim(0.9, 1.1)
axes.set_ylim(0.55, 0.65)


def neg_damped_os(t):
    return -damped_os(t)

result = minimize(neg_damped_os, 1)

# maximum arrow
x_max, y_max = result.x, -result.fun
dx, dy = 0.02, 0.03
plt.arrow(x_max - dx, y_max - dy, dx, dy,
          width=0.0001, length_includes_head=True)
plt.annotate("max", xy=(x_max - dx - 0.01, y_max - dy - 0.005))

x_tang, y_tang = 1.0, damped_os(1.0)
dx, dy = 0.03, 0.01
plt.arrow(x_tang + dx, y_tang + dy, -dx, -dy,
          width=0.0001, length_includes_head=True)
plt.annotate("tangent", xy=(x_tang + dx + 0.005, y_tang + dy))

plt.savefig('images/201405_Maximum_of_damped_free_vibrations/freedampedzoom.png')

Maximum of free damped oscillators

Summary

Code for Plots

Share this post

Similar Posts